Calculating Equivalent Time for Use in Determining the Lethality of EtO Sterilization Processes
Originally Published MDDI February 2002 STERILIZATIONCalculating Equivalent Time for Use in Determining the Lethality of EtO Sterilization Processes
 Since its introduction more than 40 years ago, EtO processing has proven very effective for the sterilization of medical products.1 Approximately 45% of the medical devices handled by contract sterilizers in the United States today are treated using an EtO process, and it remains the method of choice for products constructed from materials that are incompatible with high temperatures or radiation.
Since its introduction more than 40 years ago, EtO processing has proven very effective for the sterilization of medical products.1 Approximately 45% of the medical devices handled by contract sterilizers in the United States today are treated using an EtO process, and it remains the method of choice for products constructed from materials that are incompatible with high temperatures or radiation.
More complex than either thermal or radiation processing, EtO sterilization does present challenges to its users. Not only does it require extensive postprocess testing of products for residuals, its effects are difficult to express mathematically because the rate of microbial lethality is affected by three primary process parameters: EtO concentration, temperature, and relative humidity (RH). Methods of integrating the effects of these factors were lacking until recently, when one approach was published in this magazine (Alfredo Rodriguez et al., September 2001 MD&DI, p. 100).2 This article presents another approach, developed over the last year by researchers at Biotest Laboratories Inc. (Minneapolis), SGM Biotech Inc. (Bozeman, MT), and STS Inc. (Rush, NY). Direct and comprehensive, this work led to the achievement of simple yet broadly applicable integration methods for use in process situations.
Although many factors complicate the EtO sterilization process, including EtO absorption, product material effects, the existence of microenvironments in the process chamber, and the achievement and maintenance of steady-state conditions, this article focuses only on the three primary parameters.
The effects of these factors were studied at the researchers' laboratories using biological indicator evaluator resistometer (BIER) vessels. Designed for the calibration of biological indicators (BIs), these vessels operate within the narrow control windows defined in the domestic and international standards on EtO sterilization.3,4 The interrelated problems of calculating integrated lethality and comparing dissimilar process variables were addressed by applying known principles that have been derived from other sterilization processes.
It is hoped that the use of the equations presented here, in combination with such new technologies as the direct chamber infrared (IR) method for measuring EtO concentrations, will enable more precise integration of the complete EtO sterilization cycle than has been possible.5 The goal in developing this mathematical model for sterilization lethality was threefold:
To enable EtO processors to predict the accurate D-values and related process times necessary to achieve a sterility assurance level (SAL) of ¾ 10–6.
To provide the tools necessary to optimize process cycles by reducing cycle times and/or EtO concentrations, thereby minimizing EtO residual levels and outgassing quarantine times and maximizing process throughput.
To provide a method for quantifying integrated lethality, which will allow the industry to move toward parametric release.
BACKGROUND
It has been demonstrated that EtO concentration and temperature are independent variables and that the rate of lethality increases as either is increased. Although some researchers have reported a temperature-dependent plateau effect for EtO concentration, others have not confirmed the phenomenon.6,7 In the work reported here, data at 54°C over tested concentrations between 300 and 750 mg/L did not support the magnitude of the reported temperature-dependent plateau. In the temperature range of 27°–60°C (80°–140°F), low and high RH levels are known to reduce the effectiveness of EtO processes. The generally accepted RH control limits are ~30 and ~90%. Within that range, humidity can be considered a constant; below ~30% RH, sterilization efficacy decreases markedly, while above ~90% the potential for H2O ondensation increases. Tests conducted during this study used an RH of 60%.
The following classically accepted formulas for the application of resistance studies to process calculations are the basis for the mathematical model presented here:
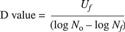 (1)
(1)
where Uf is equivalent exposure time, N0 is the initial spore population, and Nf is the final spore population.
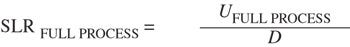 (2)
(2)
where U full process is the equivalent time for the full sterilization process.
SAL = 10 log N0–SLR (3)
CALCULATING EQUIVALENT TIME
|
Figure 1. The relationship between D-value, SLR, and SAL. The lethality delivered in any sterilization cycle, SLR is calculated as the log of the initial population (N0) minus the log of the final population (NF). The SAL, the probability of a viable microorganism being present on a product unit after sterilization, is calculated using Equation 3. |
An annex to ISO standard 11135 identifies a method for calculating process D-values, which represent the dose or time at steady state required to reduce a microbial population by 90% or 1 log10.8,9 Unfortunately, the document provides little guidance to assist users in estimating the equivalent time (U) required for such calculations. In the extreme, use of the actual exposure time (which begins after steady-state pressure has been achieved) rather than equivalent time may lead to a gross underestimation of a process's D-value and concomitant overestimation of the SLR and underestimation of the SAL. The method of D-value calculation is irrelevant to this problem. Whenever equivalent time is underestimated for D-value calculations, the result will be the same. Figure 1 demonstrates the relationship between D-value, SLR, and SAL at steady state when microbial inactivation follows a straight-line log-linear relationship.
EtO process D-value calculations have been used primarily in BIER vessel studies, where the time to steady state approaches zero and the equivalent exposure time approaches the actual exposure time. However, applying any D-value calculation method to EtO systems used for actual product sterilization is inappropriate because standard-sized process chambers do not produce square wave cycles and substantial lethality is generated during both their charge (gas injection) phase and gas evacuation phase (which do not fall within the exposure time). For steam or dry-heat sterilization systems, integrated lethality or lag correction factors can be applied.9 However, for EtO systems, no such standard methodology exists. This situation accounts for the popularity of the AAMI overkill validation technique and the equivalent ISO half-cycle method, neither of which require calculations of D-valve, SLR, or SAL.8
If the actual exposure time is used in Equation 1 rather than equivalent exposure time, then as the exposure time approaches zero when log N0 – log Nf is some positive number, then the D-value also approaches zero; subsequently, SLR approaches infinity and SAL approaches
10–¥. While no one would suggest that a D-value would equal zero, this extreme example demonstrates the dangers of underestimating the equivalent time. Adding some arbitrary number to increase U does not allow the individual responsible for process validation to know whether U and, therefore, the D-value, are still being underestimated, and if so to what extent. Overestimating the equivalent time for the full process will similarly result in an overestimation of SLR and an underestimation of SAL, although the percentage error will generally be less than when U is underestimated for D-value calculations, because the latter error is multiplicative.
|
Figure 2. The EtO sterilization cycle. |
EtO Lethality. Table I presents results from sterilization validations conducted at Biotest for a variety of medical products. These validations used an exposure time of zero minutes, yet resulted in few or no positive BIs, which is not surprising if one understands the concept of accumulated lethality. The table also includes estimated equivalent times for these zero-minute exposures, related D-values, and full-process-cycle SALs. The EtO sterilization cycle being validated in most of this testing is depicted in Figure 2. For this process, the lethality attributed to EtO begins with the injection of the gas into the process chamber. Whether pure EtO is used, as in the process shown, or a gas mixture (such as CO2/EtO or EtO and an HCFC diluent), lethality increases as the concentration increases, and the concentration increase is proportional to the pressure rise in the chamber.11 For processes with well-controlled pressure ramp-up rates, EtO concentration changes also are proportional to time during gas injection and evacuation. A cycle's exposure-time phase starts when the control pressure has been achieved, which occurs after gas injection is completed. It should be noted that, in practice, absorption, microenvironments, diffusion, and chemical reactions that consume the gas can slow the development of steady-state EtO concentrations in some process chamber locations or product areas.
Product Type | Positive BIs/Total BIs | Calculated U (min) | Calculated D-Value | Calculated Full-Cycle SAL | Full Cycle ProcessExposure Time (hr) |
Introducer, delivery forceps, catheter | 1/20 Tha | 24.65 | 3.34 Th | 1 x 1066 Th | 4 |
Occluder delivery system | 6/20 Th | 24.15 | 3.75 Th | <1 1087 Th | 5 |
Tubing sets and scopes | 5/20 Th | 24.15 | 3.69 | <1 x 1072 | 4 |
Cannula | 2/20 Stripsc | 36.9 | 5.29 | 1 x 1074 | 4 |
Catheters, introducers | 22/44 Th | 47.75 | 7.56 | 1 x 1032 | 2.5 |
Rotor blade | 17/20 Mpsd | 24.95 | 4.16 | <1 x 1051 | 4 |
Suture anchor | 17/20 Mps | 25.25 | 4.00 | 1 x 1054 | 4 |
Compass tips and magnets | 15/20 Th | 25.7 | 4.07 | 1 x 1052 | 4 |
Clamp covers, loops, brush, boots | 3/20 SC | 24.65 | 3.63 | 1 x 1060 | 4 |
Optical fiber | 0/20 SC | 24.15 | < 3.31 | <1 x 1074 | 4 |
Sensor, probe, wire, etc. | 0/20 SC | 24.65 | < 3.38 | <1 x 1065 | 4 |
Orthopedic implant product line including bone- harvesting device | 0/80 Strips | 44.9 | < 6.18 IP | <1 x 1033 IP | 4 |
Unassembled bone-harvesting device | 0/20 strips; 0/20 SC | 45.15 | < 6.19 Strips | <1 x 1032 Strips | 4 |
Injectable polymer system | 1/19 strips | 24.85 | 4.09 | 1 x 1052 | 4 |
a Th = 1.5-in. single-strand cotton thread inoculated with >1x106 B. subtilis (SGM Biotech). | |||||
Table I. Zero-minute exposure data and calculations for equivalent time (U), D-value, and SAL for validation testing of various medical products. SAL was calculated by the Stumbo, Murphy, and Cochran method.10 |
For the cycle in Figure 2, the EtO gas injection time is 11 minutes and the exhaust time is 16 minutes, which are common times in EtO processing. An 11-minute nitrogen (N2) overlay immediately follows the EtO injection phase; hence EtO concentration is at its maximum during that period. Data such as these can be converted to equivalent time for D-value, SLR, and SAL calculations using the mathematical model described below. The technique is based on lethality rate (LR), which can be expressed either as a rate function with units of Dlog N per minute at specified conditions or as the reciprocal of the D-value.
|
Figure 3. Log/linear plot of D-values versus EtO concentration. |
Parameters affecting EtO sterilization have been studied extensively and numerous investigators have shown that microbial D-values decline as EtO concentration increases.1,7,12–16 These observations were verified by recent studies at SGM Biotech in which sets of BIs were tested at EtO concentrations of 300, 450, 600, and 750 mg/L. Three lots each of standard spore strips and the company's self-contained EZ Test were tested in an EtO BIER vessel from Joslyn Valve (Macedon, NY). Comparative D-values from the studies are listed in Table II. Test results also are graphed on a log10/linear plot in Figure 3, which indicates there were reasonable straight-line fits with R2 values of 0.9695 and 0.9909 for spore strips and the self-contained test, respectively. However, Figure 4, which is a linear/linear plot of both D-values and lethality versus EtO concentration for spore strips, depicts a more useful relationship.
Lot No. | Log Spore Population | BIType | Ethylene Oxide Concentration (mg/L) |
300 | 450 | 600 | 750 |
D-value | |||
G-92P | 6.531 | Self-contained test | 5.8 |
G-103P | 6.322 | 5.6 | 4.2 |
G-105 | 6.255 | 5.2 | 4.0 |
Average | NA | 5.5 | 4.1 |
BSUB-235 | 6.398 | Paper strips | 6.7 |
BSUB-244P | 7.0 | 6.2 | 4.4 |
BSUB-249P | 6.398 | 6.1 | 4.1 |
Average | NA | 6.3 | 4.3 |
Table II. Comparative D-values at four EtO concentrations calculated using the Spearman-Karber method.17 These test results are also shown graphically in Figures 3 and 4. |
|
Figure 4. Linear/linear plot of D-value and lethality versus EtO concentration. |
The Microsoft Excel program for best fit of data predicts that, when plotted against EtO concentration (C), the D-value predicts a parabolic curve. As C approaches zero, then D will approach infinity. Logically it follows that EtO-associated lethality (1/D) must approach zero as C approaches zero, creating an intersection on the lethality rate plot at x = 0, y = 0; where D = 1/LR, as LR approaches zero, then D approaches infinity, which also is predicted by the plot of D, which is asymptotic in both directions, or hyperbolic. Thus a linear/linear plot of the lethality rate allows a simple approach to calculating equivalent time if temperature is considered to be constant:
LR ~ C, or LR = kC (4)
where k is the rate constant. The equation can also be expressed
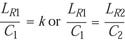
and so on. Solving for LR,
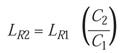
Since the D-value is a reciprocal of the lethality rate, the equation can also be used to solve for D:
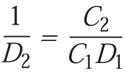 (5)
(5)
which simplifies to:
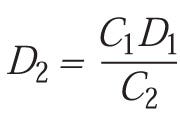
LR may also be used to derive Dlog N as a function of time (t) where:
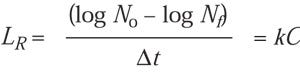 (6)
(6)
log No – log Nf = kC Dt
To calculate accumulated lethality at a constant temperature (T1), each increment is multiplied by the time at that increment, which is expressed in the summation formula:
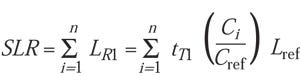 (7)
(7)
|
Figure 5. Cumulative lethality (SLR) of standard versus ramped BIER cycles, at constant temperature. |
Testing the Models. As the next step in this research project, testable hypotheses based on the theoretical application of these concepts were developed. That is, that at a constant temperature, lethality can be calculated based on time-weighted EtO concentrations, and equivalent time at steady state can be approximated for those phases of sterilization where concentration changes are proportional to time by dividing real time by two. Testing was performed at STS using a BIER vessel that could be ramped up over 10 equal pressure steps of 60.6 mg/L. Adjustment time between steps was 5–6 seconds for a total injection time of 50–60 seconds, which is the same as that used for a standard cycle performed using the same BIER unit. The exhaust phases for the ramped and standard cycles were also equal. The hold time at each step for the ramped cycles was varied to provide a time-weighted average EtO concentration that was equal to that of a standard cycle. For example, to simulate a 30-minute standard cycle, a ramped cycle was performed using hold times of 6 minutes at each of the first 9 steps and 3 minutes at the last (606-mg/L) step. This provided a time-weighted average of 18,810 mgxmin/L the same as achieved with a standard 30-minute cycle in that BIER unit, with no adjustment for charge and discharge phases. This relationship is shown in Figure 5.
Five lots of BIs, representing three different manufacturers and three different BI types, were processed using comparable ramped and standard BIER cycles. Three of the lots were standard BI strips, each from a different manufacturer. These strips were all cultured in the same lot of Trypticase soy broth from BBL Inc. (Syracuse, NY). Media for the other two lots, which were self-contained EZ Test and Releasat BIs from SGM Biotech, are part of the BI systems. Standard conditions for the test cycles were a constant temperature of 54° ± 1°C, EtO concentration of 600 ± 30 mg/L, and RH of 60 ± 10%. The fraction-negative results of these tests are given in Table III, and the resulting D-value calculations are listed in Table IV. As the tables indicate, the results for the two methods of gas exposure were extremely close and certainly within the ±20% recommended by USP XXIV for verification of D-values.18 Furthermore, no strict bias was evident suggesting a random variation. These data support formulas 4 and 5.
BI Type | Cycle No. | Log No. | EtO BIER Cycle |
15 min | 20 min | 22.5 min | 25 min |
Std. | Ramped | Std. | Ramped |
No. of positive BIs out of 10 total | |||
EZ Test | 1 | 6.380 | 10 |
2 | 00 | 00 | 10 |
Releasat | 1 | 6.176 | 10 |
2 | 00 | 00 | 3 |
Strips | 1 | 6.301 | 10 |
2 | 00 | 00 | 10 |
Strips | 1 | 6.342 | 10 |
2 | 00 | 00 | 10 |
Strips | 1 | 6.447 | 10 |
2 | 00 | 00 | 10 |
Table III. BI fraction/negative results from testing using comparable ramped and standard BIER vessel cycles. |
BI Type | Log No. | EtO BIER Cycle |
Std. | Ramped | Ramped, % Deviation from Std. |
D-Value | 0 | |
EZ Test | 6.380 | 3.39 |
Releasat | 6.176 | 3.10 |
Strips | 6.301 | 3.48 |
Strips | 6.342 | 3.53 |
Strips | 6.447 | 3.62 |
Average | NA | 3.42 |
Table IV. Calculated D-values for tests using comparable ramped and standard BIER vessel cycles. The Stumbo, Murphy, and Cochran calculation method was used.10 This D-value was recalculated assuming one negative at 22.5 minute and one positive at 25 minutes because all units were positive at 22.5 minutes, even though one negative was observed at 20 minutes and all units were negative at 25 minutes. This D-value was also recalculated assuming one positive at 25 minutes to assure comparable treatment of the standard and ramped cycles for this BI type. |
Accounting for Temperature Variations. The work described thus far focused on EtO lethality at a constant temperature. A technique for calculating the effect of temperature variations on D-values—known as the z-value effect—has been described for steam and dry-heat applications.19 To account for such an effect on EtO sterilization, the researchers involved in this study consulted a range of sources.2,6,7,11–15 One reported a theoretical lower limit of Q10 = 1.8 for EtO sterilization,14 but a consensus seems to have evolved for a nominal Q10 value of 2. (This means that a 10°C change would affect lethality by a factor of 2.) Thus a Q10 value of 2 was used for a set of temperature-related tests along with a z value of 33.2°C, which was calculated using the relationship z = 10°C/log10 Q. This value was intermediate between a recently suggested z value of 36°C and an older recommendation of 29.4°C.15,9 After the test results (which are described below) were reviewed, however, it became apparent that the best choice of z to fit the experimental data is 29°C, which is essentially the result for a Q10 value of 2.21 and very close to the calculated value of 29.4°C suggested by another previous study.11
Because they are independent variables, a reference EtO concentration (Cref) and temperature (Tref) can be used to calculate the equivalent time for various temperatures as follows:
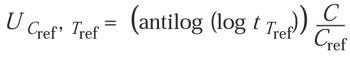 (8)
(8)
where
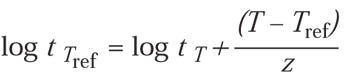
For example, using z = 29°C, if the exposure time (t) is 40 minutes, the temperature (T) is 40°C, and the concentration (C) is 300 mg/L, the equivalent time at Cref = 600 mg/L and Tref = 50°C is 9 minutes:
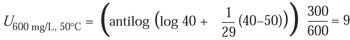
In addition, because D ~ U, the above equation also can be used to address D-value:
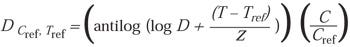 (9)
(9)
To determine accumulated equivalent time where conditions are changing for EtO concentration and/or temperature, a summation equation can be applied:
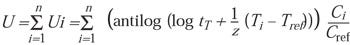 (10)
(10)
Dref | Derivation | BI Lot No. 235 | BI Lot No. 244 | BI Lot No. 249 |
DC600°, T54 | Empirical | 3.5 | 3.4 | 3.4 |
DC750°, T40 | Empirical | 8.5 | 7.8 | 8.6 |
Calculated | 8.5 | 8.3 | 8.3 | |
DC600°, T45 | Empirical | 7.4 | 6.6 | 7.1 |
Calculated | 7.2 | 6.9 | 6.9 | |
DC300°, T60 | Empirical | 4.7 | 4.4 | 4.3 |
Calculated | 4.3 | 4.2 | 4.2 | |
Table V. Empirical and calculated D-values for three lots of BIs processed at various EtO concentrations and temperatures. D-values were calculated using the Spearman-Kaber method.17 |
To test the applicability of Equation 9, BIs from three lots were processed using various EtO concentrations and temperatures at SGM Biotech. The test conditions were: (1) 60°C, 300 mg/L EtO, and 60% RH; (2) 40°C, 750 mg/L EtO, and 60% RH; and (3) 45°C, 600 mg/L EtO, and 60% RH. The empirical D-value results from these tests are shown in Table V, along with the D-values that were calculated from the original lot certifications at the standard BIER conditions of 54°C, 600 mg/L EtO, and 60% RH. In all cases, the empirical and calculated values agreed closely.
Consideration of the Rodriguez Article. Because it addressed the same issue as the research reported here, the article by Rodriguez et al. was considered carefully.2 One point raised was that the Rodriguez equation for calculating survivors after the first time increment (Dt) is not obvious since the natural log (ln) is used:
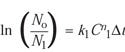 (11)
(11)
However, by deferring to the first-order theory of inactivation20 and comparing this equation with Equation 6 above, it was determined that the empirically determined rate constants (k) for the two studies (designated R for Rodriquez and M for Mosley) are related in the following way:
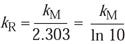 (12)
(12)
Therefore, it was concluded that the two equations are equivalent. Based on the rate constant relationship, it was also determined that Equation 6 correlates to the Rodriguez equation for the relationship among D, k, and C:
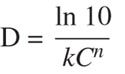 (13)
(13)
since
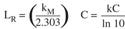
Another issue that was considered involved the final integration equation in the Rodriguez article.
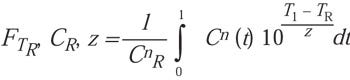 (14)
(14)
The current authors agree that the equation is mathematically correct but believe it is unusable in the given format because the EtO concentrations presented in the Rodriguez article cannot be defined by any reasonable equation. In addition, no solution for Cn was given, although n = 1 was suggested. However, in the model validation section that followed, a summation formula was used in the software work-sheet that transforms to Equation 10 in this article. This final transformation essentially completes a mathematical proof of the two approaches. It was concluded that the independent work reported here confirms the equations proposed by Rodriguez and vice versa.
RECOMMENDATIONS FOR APPLYING THE MODEL
When using the general formulas for calculating process lethality (Equations 1–3), it is critical that equivalent time is not underestimated in Equation 1 or overestimated in Equation 2 because of the effect on SAL. However, the use of approximations or estimations is unavoidable, and a large error is always worse than a small one. Depending on the metrology systems available to particular users, several approaches to maximizing the usefulness of these equations are possible.
For all of the equations, the reference temperatures, concentrations, D-values, and LR values should be for the target control conditions. In addition, whether it results from absorption, chemical reactions, or penetration or diffusion lags, any delay in achieving the expected EtO concentration within the load or product will lead to a calculated U that is greater than the actual U. Therefore, if estimations of product EtO concentration are based on theoretical levels related to EtO pressure rise, equivalent time will be overestimated. On the other hand, a nitrogen overlay may produce a very short period of higher-than-predicted EtO concentrations in the product, and if this phenomenon is not considered the equivalent time will be underestimated.
Total Integration. Ideally, metrology systems capable of monitoring EtO concentrations within the load and the product would provide the most accurate and complete data. However, the available techniques for monitoring product EtO concentrations involve the active withdrawal of samples into a gas chromatograph or IR analytical system, and the act of sampling changes the concentration at the location of interest. The next best approach is to monitor the chamber EtO concentration and combine that data with product temperature data. Inputting these data incrementally would allow the data acquisition system to calculate cumulative equivalent time for the full process, as well as for the shorter cycles used in D-value calculations. Product release criteria could then be established based on total equivalent time as established in the validation.
Estimated Integration. EtO concentrations can be estimated based on the pressure differential in the chamber during the various sterilization cycle phases. These phases include EtO injection time, nitrogen overlay time (where appropriate), exposure time, and the time from the start of exhaust to the inflection point. EtO concentration will decrease during the exposure-time phase unless a pure EtO cycle is used and makeup gas charges are performed to maintain pressure throughout the period. Because this decrease is due to the preferential absorption of EtO by the product materials, regardless of which other gases are present in the chamber, the changes in concentration can be estimated. Decreases in EtO concentration should be directly proportional to decreases in pressure differential. In the case of gas mixtures, any makeup charges will contribute the proportional amount of EtO present in the mixture to the overall EtO concentration in the chamber.
Simple Approaches. If a system for determining changes in chamber EtO concentration is not available, a reasonable over-estimation of equivalent time can be made for use in Equation 1 by applying the following formula (or sections thereof as appropriate):
 (15)
(15)
This approach can also be used to estimate U without regard to changes in temperature. During the early stages of the process cycle, temperatures are below the target level. If increasing temperature is taken into account, the estimated equivalent time will be lower than if temperature is treated as if it were at steady state throughout the cycle. With regard to both EtO concentration and temperature, therefore, the overestimates that result from using this simplified approach will result in the use of full process cycles that are longer than necessary to achieve the required SAL of ¾ 10–6.
In contrast, when equivalent time is used in Equation 2 for the full process, it is critical to ensure it is not overestimated. Obviously, the more actual temperature and EtO concentration data that can be included in the calculations, the better, but any justifiable estimating method that leads to overestimates of D-value and SAL is acceptable. A common approach for estimating U for the full process is to disregard the equivalent time contributed by the cycle phases prior to and following the exposure-time phase. The equivalent time contributed during those phases then becomes an added safety factor. Another, more-accurate approach would be to double the equivalent time calculated for a half cycle by including the EtO injection, nitrogen overlay, and evacuation time periods.
|
Figure 6. EtO sterilization lethality at two locations where temperatures are 10°C apart. |
The Boundaries Approach. It has also been suggested that the use of boundaries may be appropriate for estimating equivalent time for EtO sterilization.21 One approach is to consider the variations in temperature within the chamber. Figure 6 plots the expected change in log N over time during an EtO process where both EtO concentration and temperature are increasing. The concave curves seen in the figure represent the rate of microbial lethality at two locations in the chamber that differ in temperature by 10°C. Assuming a Q10 of 2, the rate of microbial population decrease will differ by a factor of 2 between these two locations. The higher-temperature boundary can be used to estimate equivalent time for D-value calculations and the lower-temperature boundary to estimate it for determining the full process SLR.
It should be noted that the Pflug and Holcomb method for D- value calculations may be inappropriate in some situations.9 One of its primary advantages is the accurate determination of mean time until sterility. For processes where all-zero or only fraction-negative results are obtained for the shortest possible EtO exposure cycle, the method cannot be used. In such situations the Stumbo, Murphy, and Cochran method for lethality calculations is recommended.10
CONCLUSION
The equations presented here, along with other recently published formulas on accumulated and integrated lethality for EtO process sterilization, have been developed to assist practitioners involved in validation and routine product release. When temperature data are used in conjunction with direct EtO concentration measurements, the prospects for moving toward parametric release are enhanced. This approach will also normally lead to shorter cycles than have been possible using older methodologies or in cases where equivalent time for the full process has been overestimated.
ACKNOWLEDGEMENTS
The authors wish to thank Irving Pflug, Carl Bruch, Duane Hass, and Richard Holcomb for their helpful suggestions and for reviewing portions of this manuscript.
REFERENCES
1. CW Bruch, "Gaseous Sterilization," Annual Review of Microbiology 61 (1961): 245–262.
2. AC Rodriguez et al., "Calculating Accumulated Lethality and Survivorship in EtO Sterilization Processes," Medical Device & Diagnostic Industry 23, no. 9 (2001): 100–107.
3. BIER/EO Gas Vessels, ANSI/AAMI ST44:1992 (Arlington, VA: Association for the Advancement of Medical Instrumentation [AAMI], 1992).
4. Sterilization of Health Care Products—Biological Indicators—Part 2: Biological Indicators for Ethylene Oxide Sterilization, ISO 11138-2:1994 (Geneva: International Organization for Standardization, 1994).
5. PG Smith, "Continuous Monitoring of EtO Concentrations during Sterilization," Medical Device & Diagnostic Industry 23, no. 2 (2001): 80–88.
6. DJ Burgess and RR Reich, "Industrial Ethylene Oxide Sterilization," in Sterilization Technology: A Practical Guide for Manufacturers and Users of Health Care Products, ed. RF Morrissey and GB Phillips (New York: Van Nostrand Reinhold, 1993), 152–195.
7. K Kereluk et al., "Microbiological Aspects of Ethylene Oxide Sterilization," Applied Microbiology 19 (1970): 157–162.
8. Medical Devices—Validation and Routine Control of Ethylene Oxide Sterilization, ISO 11135:1994 (Geneva: International Organization for Standardization, 1994), 11–16.
9. IJ Pflug, RG Holcomb, and MM Gomez, "Thermal Destruction of Miroorganisms," in Disinfection, Sterilization, and Preservation, ed. S Block (Philadelphia: Lippincott, Williams & Wilkins, 2001), 79–129.
10. CR Stumbo, JR Murphy, and J Cochran, "Nature of Thermal Death Time Curves for P.A. 3679 and Clostridium botulinum," Food Technology 4 (1950): 321–326.
11. TS Lui et al., "Dichlorodifluoromethane—Ethylene Oxide Sterilization as a Sterilant at Elevated Temperatures," Food Technology 22 (1968): 86–89.
12. JR Gillis, "Cycle Development—Microbial Challenge Systems," in Industrial Ethylene Oxide Sterilization of Medical Devices—Process Design, Validation, Routine Sterilization, AAMI Technological Assessment Report No. 1-81 (Arlington, VA: AAMI, 1981), 21–22.
13. JR Gillis, "Ethylene Oxide Sterilization," in Validation of Aseptic Pharmaceutical Processes, ed. FJ Carleton and JP Agalloco (New York: Marcel Dekker, 1986), 357–376.
14. RR Ernst, "Ethylene Oxide Gaseous Sterilization for Industrial Applications," in Industrial Sterilization, International Symposium, Amsterdam 1972, ed. GB Phillips and WS Miller (Durham, NC: Duke University Press, 1973), 181–208.
15. CW Bruch "Ethylene Oxide Sterilization—Technology and Regulation," in Industrial Ethylene Oxide Sterilization of Medical Devices—Process Design, Validation, Routine Sterilization, AAMI Technological Assessment Report No. 1–81 (Arlington, VA: AAMI, 1981), 3–5.
16. LJ Joslyn, "Gaseous Chemical Sterilization," in Disinfection, Sterilization, and Preservation, ed. SS Block (Philadelphia: Lippincott, Williams & Wilkins, 2001), 337–359.
17. RG Holcomb and IJ Pflug, "The Spearman-Karber Method of Analyzing Quantal Assay Microbial Destruction Data," in Selected Papers on the Michobiology and Engineering of Sterilization Processes, ed. Irving J. Pflug (Minneapolis: Enviromental Sterilization Laboratory, 1988), 83–100.
18. "Biological Indicator for Ethylene Oxide Sterilization, Paper Strip," in US Pharmacopeia XXIV (Rockville, MD: United States Pharmacopeial Convention, 1999), 231–232.
19. IJ Pflug, Microbiology and Engineering of Sterilization Processes, 10th ed. (Minneapolis: Environmental Sterilization Services, 1999).
20. O Rahn, Injury and Death of Bacteria by Chemical Agents, Biodynamica Monograph No. 3, ed. BJ Luyet (Normandy, MO: Biodynamica, 1945), 9–41.
21. IJ Pflug and R Holcomb, personal communication with the authors. October 23, 2001.
Illustration by Bek Shakirov
Copyright ©2002 Medical Device & Diagnostic Industry
About the Author(s)
You May Also Like