Design of Experiments with Process Signature Verification
Process signature verification is a technique that is new to many medical device companies. Here is how to do it.
PROCESS CONTROL
Process signature verification (PSV) is the ability to analyze process signatures based on physical parameters. The PSV technique gives manufacturers detailed information about what is happening during a physical process involved in manufacturing. That process can be a test of a product or a manufacturing or assembly step. The point is that some physical action is being taken, and the state of a physical parameter is being changed. For the purpose of this article, the process examined is a force being used to compress a spring to a certain depth.
PSV is the comparison of a detailed and specific process variable response against predetermined responses. Those responses can indicate process compliance with specifications, or they can indicate the presence of monitored failure modes. The purpose of PSV is to provide an empirical and objective way to determine the success or failure of a manufacturing operation.
The information derived from the process signature is a track of the real-time change of the state of the parameters that are being measured. In this case, the parameters are the force on the spring and the distance compressed. The process signature provides a detailed picture of how the system responds to the operation.
The experiment uses tracking at 5000 points per second, or every 0.2 millisecond. This data rate is far more than adequate for such a simple system. It is usually better to start experiments at a higher data collection rate initially. Up to 100,000 samples per second may be reasonable, depending on the manufacturing operation that is being monitored. The goal is to see as much subtle difference as possible in the curves. Once the speed at which important effects happen is determined (in an electronic system, this would be equivalent to frequency), an operator may choose to back off the collection rate or to maintain the full-frequency information content. The eventual results will be achieved by learning how to derive subsecond manufacturing line speeds with maximum data depth.
Traditionally, statistical process control (SPC) is defined as the application of changes to a process to keep it from going outside the boundaries set for a successful operation based on a physical measurement. In practice, this generally means discarding products that do not meet specifications.
PSV significantly extends the capability of statistical control. SPC and statistical analysis enable manufacturers to precisely measure an effect, and PSV gives a detailed overview of a process to allow the extension of what, where, and how to measure.
SPC is based on single-point measurements applied to each part as it comes through the manufacturing line. These measured points provide a mathematical way to determine whether any behavior indicators denote out-of-spec conditions.
In PSV, measured points are identified within the signature curve once these points are proven to be consistently reliable indicators of results. The result could be an indication of the presence of a failure mode, or some change in the part that is specified. The purpose of the numerical analysis is first to determine whether a failure mode can be caught with 98% confidence, and then to do so.
|
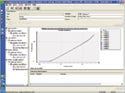
Figure 1. (click to enlarge) An original data curve from a design of experiments of 13 runs and multiple independent variables. |
What SPC doesn't provide is an indication of where to look or what to look for. This is a critical point. If an operator does not know where to look for a failure mode, it may never be found. For example, Figure 1 shows the original data curve from a sophisticated design of experiments (DOE) of 13 runs and multiple independent variables. More than 3000 sample signature curves were collected.
There were clearly noise frequencies in the initial sample. So, a frequency analysis was performed to determine what information related to the process and what related to noise in the system. In this case, machine vibration caused the noise.
|
Figure 2. (click to enlarge) After the unwanted frequency response is removed, the curve shows how a system actually behaves. |
To see the underlying process signature of the system, the unwanted frequency response caused by machine vibration was then removed. At that point, the manufacturer could see exactly how the system behaved (see Figure 2). With these signatures, several areas become obvious candidates for analyses that could lead to useful monitoring algorithms.
With a picture of what actually happened in the system, an algorithm can be devised to find the behavior that needs to be monitored. The result of that algorithm is a number. It should be checked, using statistical means, for its ability to accurately predict a fault or defect.
|
Figure 3. (click to enlarge) A view of adequately separated failure modes that occurred during process signature verification. |
The results from a successful algorithm are ultimately used to determine and then to measure pass-fail criteria on the manufacturing line. In essence, it delivers process verification. Without the pictures, it would be impossible to determine where and what to measure. On the other hand, without the statistics, it would be impossible to have any degree of certainty that the chosen curve feature reliably indicates the investigated failure modes (see Figure 3). The signatures and the statistical analysis work hand in hand.
The second important issue to address at the outset is sensor placement. It is one of the most important aspects of getting a good physical measurement, and it is often overlooked. When beginning to analyze a physical process, it is important to start by collecting the best possible data, which means attention to sensor choice and placement. The sidebar (Important Considerations for Sensor Choice and Placement) lists some considerations for sensors.
The Experiment
For this article, the experiment is a simple one in which a spring is compressed from a 4-in. length to a 2-in. length using a 200-lb force constant. The parameters that are monitored are force applied and distance traveled.
A spring is a simple system, but finding defects can have direct applicability to product quality. For instance, spring response to force will change if there are variations in wire diameter or if the material composition changes. Also, manufactured springs can be different lengths without the variations being visible to the eye or practical to check individually. In the tight geometries of medical devices, exact length makes a difference. In this example, manufacturing debris can also affect the way a spring responds to force.
Testing a spring system in process allows manufacturers to avoid an impossible or impractical end-of-line test while verifying the behavior of each system individually.
|
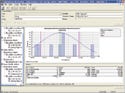
Table I. (click to enlarge) A sample process chart. The parameters are examples of measurements taken during process signature verification. |
Finally, although this simple system provides a clear introduction to how to begin to analyze process signatures, PSV is applicable to most common manufacturing processes and methods. The sample process chart in Table I provides a starting point for some common manufacturing processes.
This test uses a press with two integral sensors, a load cell that can measure up to 1000 lb sited directly on the mechanism pushing the spring and a linear-displacement transducer inside a moving servo-driven ram. The system zeroes itself after every press.
Method
To initiate testing, several good presses are run, in which the spring is correctly fitted into the test jig and there are no defects. These runs create the standard, or specification, signature for the operation. Once that signature is created, a series of deliberately created defects are prepared. The defects are created by putting antistatic matting between several coils of the spring (to represent debris) and by misaligning the spring on the test jig. The task is to determine where the defects are indicated in the signature. In addition, an algorithm should be devised that delivers an acceptable measurement of what will be seen as bad outcomes to verify the process. It's a simple operation, and all steps are the same for each experiment.
Process
|
Table II. (click to enlarge) An example of a testing scheme. |
When designing an experiment with PSV, it is important to keep in mind that the data need to be easily separated into useful buckets of information. To do that, it is crucial to think about data design. This experiment uses the scheme shown in Table II. It's a good idea to set up the testing system so that runs can be selected independently for analysis to compare the effects with each other. The easiest way to do this is by identifying a run with a model number in the measurement system. So, for this example, these model numbers are used for this trial: Good_Part, 1_Test, 2_Test, and 3_Test.
Some systems allow users to store an almost unlimited number of variable settings. With such systems, users can slice and dice their data many ways. Because the purpose of this analysis is to analyze the data for a limited number of variables, the study is considerably simplified.
|
Figure 4. (click to enlarge) The good spring appears to be free from defects, because the trail result looks like a flat curve. |
Figure 4 provides a view of the raw data for the good spring. Initially, there is not much to see. The spring appears to give a very flat curve. However, it is known that there are defects in this operation. At the outset, they are invisible. So the question becomes, how and where to begin to look at these data to determine whether the defects can be found.
|
Figure 5. (click to enlarge) To find defects, it is important to isolate the correct portion of the curve for evaluation. |
The first step is to smooth out the hysteresis and then to isolate the correct portion of the curve for evaluation (see Figure 5). In more-complex data, such as those presented in Figure 1, other steps may be needed. Removing certain frequency ranges, looking at a derivative, smoothing, or other mathematical preprocessing steps may be needed to present a clear picture of a real waveform without noise.
The next step is to select a segment of the waveform to analyze (see Figure 6). It is important to note that, for this example, an interesting segment in the Figure 5 waveform, is where the force curve varies on the return of the spring. This segment was ignored for simplicity and to focus analysis on a more-subtle area. In an actual DOE, anything that indicates nonrepeatability should be investigated.
|
Figure 6. (click to enlarge) After isolating a portion of a curve, a segment of the waveform should be selected to analyze. |
Next, having chosen the part of the curve to investigate, different DOE runs are overlaid to see what information they give. In Figure 7, each color represents a different trial. With this representation, there is some immediate visual indication of what is happening.
|
Figure 7. (click to enlarge) Each color represents a different DOE trial. Each trial provides different information. |
Most of the defect indication is at the right-hand side of this curve. Figure 8 shows an expanded view of that part of the curve. This expanded view shows a couple of items. The first is clearly the different force levels required to compress the spring, which is expected from the physics of the problem. When extra material is inserted into the spring, an increase in force is expected. The blue curves are the good parts. Second, however, there is a change in slope in the defective curves, most obviously visible in the orange and green sets, which have the defect at the lower part of the spring. This means it is essential to have some way to determine not only that there is debris, but also where that debris is.
|
Figure 8. (click to enlarge) After isolating a portion of a curve, a segment of the waveform should be selected to analyze. |
One analysis that suggests itself is simply to look at the height of the curve, representing the amount of force applied at the point of most separation. An algorithm was created to find the height of the curve at the distance of 1.6 in. on this curve. It shows how much force is required at that point to push down a spring with and without pieces of antistatic mat. The histogram in Figure 9 shows the distribution of y at x for a single set of curves, the final set with two pieces of matting in the lower-coil position.
|
Figure 9. (click to enlarge) A histogram shows the x and y distribution for a single set of curves. |
When the results for each trial are overlaid, it is possible to see how the measurement separates the groups (see Figure 10). The blue group at the left-hand side is the control group of good parts. That makes sense because without extra antistatic mat inserted, it should take less force to push down the spring. This means that there is a number that can be measured, after appropriate preprocessing, to provide a good part–bad part result. In other words, there is good separation between good and bad parts. Good separation occurs when statistical analysis shows that each population is fully separable from the control population for a study.
|
Figure 10. (click to enlarge) When trial results are overlaid, the measurement separates the groups into the good parts and the bad parts. |
However, it would be better to go further and identify the defect types. In two of the three cases, the investigated defects nearly overlap, meaning that there is no way to distinguish between them yet.
|
Figure 11. (click to enlarge) To identify a type of defect, go back to the waveforms and consider whether another algorithm would be useful. |
At this point, it is a good idea to go back to the waveforms to see whether another algorithm will help (see Figure 11). With a closer look at the two types of defect that line up, it becomes apparent that there is a clear change in slope with one of them.
Again, the physical changes make sense. An antistatic mat is inserted in different coils of the spring. The force required to compress the spring will change at different places depending on where the antistatic mat is placed. And when the histograms of the resulting slope are examined (see Figure 12), there is clear separation between the two defects. (Only the curves from the two groups of interest are displayed so that the differences between them are clearer.)
|
Figure 12. (click to enlarge) A histogram of the slope of the second set of results shows a clear separation between defects. |
This study required two separate kinds of analysis to get to the correct identification and specific identification of each of the defects. However, these analyses yielded algorithms that can be used in manufacturing to verify the existence or nonexistence of anticipated failure modes.
Conclusion
When doing a process signature verification, it is important to be able to trace the results back to first principles. Unless there is a reasonable physical explanation for a result, it may be that there is noise in the system or some artifact of mathematics. In every case, there should be an explanation of, for example, why a change in slope represents a defect.
It is also important to remember that, although the debris-based failures were found in the example, it does not mean that every possible failure was isolated. Changes to the standard curve would be easily visible if the spring were incorrectly set into the test jig, or if a spring with the wrong constant were used. Collecting a full waveform continues to be important, even when the known failure modes have been found.
With the full waveform for each part that passes through an operation, manufacturers have a good chance of uncovering unanticipated failure modes that show up after the parts have been passed on downstream in manufacturing or to a customer. If the original data curves are available, it is possible to recheck different areas of a curve to try to find the newly uncovered problem. Once found, an algorithm can be defined to remove the problem from manufacturing.
Laura Dierker is market segment manager, life sciences, at Sciemetric Instruments Inc. (Kanata, ON, Canada), and can be contacted at [email protected]. Drew Wilson is director of technology and business development at ATS Automation Systems Inc. (Cambridge, ON, Canada).
Copyright ©2007 Medical Device & Diagnostic Industry
About the Author(s)
You May Also Like













.png?width=300&auto=webp&quality=80&disable=upscale)
